Собственно задача следующая. Необходима аппроксимация передаточной функции с предсказуемой и контролируемой нелинейностью. И в таком виде, что бы нелинейность было удобно задавать.
Т.е. у нас, например, есть каскад усиления. Он нелинеен и сам по себе имеет
заданные 2, 3, ...n-ную гармоники. Которые мы можем установить независимо друг от друга.
Т.е. эти функции гармоник должны быть ортогональны. В данном случае ортогональность означает независимость амплитуды одной гармоники от другой.
Для чего это может быть полезно?
Ну например мы хотим охватить такой каскад частотно зависимой ОС и посмотреть как это влияет на амплитуду каждой из гармоник. И будет ли ОС изменять частотный состав исходных гармоник. Или как поведут себя комбинационные частоты, попадающие в интересующий диапазон частот. При этом можно будет исследовать поведение комбинационных продуктов при известной аппроксимации исходной нелинейности и заданной частотной зависимости петлевого усиления.
В принципе для этого можно попробовать воспользоваться обычными степенными функциями. Это ещё как то работает для 2-ой и 3-ей степени. Но для гармоник более высоких порядков пользоваться простыми степенными функциями очень не удобно, так как при использовании 5 степени, например, возникает 3-я гармоника с амплитудой значительно большей амплитуды 5-ой, да и нормирование представляет проблему.
Т.е. простые степенные функции не ортогональны.
Для решения этой проблемы можно воспользоваться полиномами Чебышева первого рода,
одним из замечательных свойств которых является ортогональность.
При этом, если посмотреть на тригонометрическое определение, функция n-ного порядка является представлением n-ной гармоники.
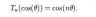
В рекурсивном виде, это может быть представлено в следующем виде:

Для проверки работоспособности была создана ЛТСПАЙС модель зависимого источника с использованием Чебышевских функций.
Модель генерит 5 первых гармоник и позволяет сравнить работу обычных полиномов и полиномов на базе функций Чебышева первого рода.
При желании в модель легко добавить более высокие гармоники используя рекурсивную формулу, приведённую выше.
Немного более подробно о полиномах Чебышева - http://ru.wikipedia.org/wiki/%D0%9C%D0%B...0%B2%D0%B0
Т.е. у нас, например, есть каскад усиления. Он нелинеен и сам по себе имеет
заданные 2, 3, ...n-ную гармоники. Которые мы можем установить независимо друг от друга.
Т.е. эти функции гармоник должны быть ортогональны. В данном случае ортогональность означает независимость амплитуды одной гармоники от другой.
Для чего это может быть полезно?
Ну например мы хотим охватить такой каскад частотно зависимой ОС и посмотреть как это влияет на амплитуду каждой из гармоник. И будет ли ОС изменять частотный состав исходных гармоник. Или как поведут себя комбинационные частоты, попадающие в интересующий диапазон частот. При этом можно будет исследовать поведение комбинационных продуктов при известной аппроксимации исходной нелинейности и заданной частотной зависимости петлевого усиления.
В принципе для этого можно попробовать воспользоваться обычными степенными функциями. Это ещё как то работает для 2-ой и 3-ей степени. Но для гармоник более высоких порядков пользоваться простыми степенными функциями очень не удобно, так как при использовании 5 степени, например, возникает 3-я гармоника с амплитудой значительно большей амплитуды 5-ой, да и нормирование представляет проблему.
Т.е. простые степенные функции не ортогональны.
Для решения этой проблемы можно воспользоваться полиномами Чебышева первого рода,
одним из замечательных свойств которых является ортогональность.
При этом, если посмотреть на тригонометрическое определение, функция n-ного порядка является представлением n-ной гармоники.
В рекурсивном виде, это может быть представлено в следующем виде:
Для проверки работоспособности была создана ЛТСПАЙС модель зависимого источника с использованием Чебышевских функций.
Модель генерит 5 первых гармоник и позволяет сравнить работу обычных полиномов и полиномов на базе функций Чебышева первого рода.
При желании в модель легко добавить более высокие гармоники используя рекурсивную формулу, приведённую выше.
Немного более подробно о полиномах Чебышева - http://ru.wikipedia.org/wiki/%D0%9C%D0%B...0%B2%D0%B0